T检验在excel中的使用
T检验在excel中的使用
.
在Excel中对两组数据做差异显著性检验是我们经常会用到的方法,多数使用者都理解并熟练其原理和使用方法的,但可能也有少数人,尽管会用各种软件来做差异性检验,但对其背后的数理并不完全清楚,比如说我自己。前段几天有人问到我,我支支吾吾给讲了个大概,发现自己好多细节并不清楚,后来经过搜索文章后,我才大致有一个相对清晰的认识,现在我把它写下来,以供诸君参考。
差异显著性检验是统计假设检验的一种,用于比较两组或多组数据之间的差异是否显著。它有好几种类型,包括t检验,u检验,卡方检验以及方差分析等,我们这里只讨论t检验。
但在讲述t检验之前,我们需要先了解中心极限定理,小概率事件等概念做一个简单的回顾复习,这会更好地帮助我们理解差异显著性检验背后的逻辑。
中心极限定理
什么是中心极限定理,中心极限定理指的是在一定条件下,独立随机变量的期望随着样本量的增大会趋向于正态分布,也就是说,它的累计分布函数会收敛于标准正态分布。
换句话说,不管总体样本是什么分布,当样我们任意从总体样本中抽取足够大的样本时,这些被抽样的样本均值都会围绕在总体样本的均值周围,并且呈正态分布。
如果再具体一点说,就是对某一个总体样品数据中进行放回随机抽样,每次抽取样本数量为n,抽了k次,则每次抽样得到的均值是m1,m2,m3,……,mk。这时候我们会发现,这些抽样样本的均值(即m1,m2,m3,……,mk)是满足正态分布的,这就是中心极限定理。
中心极限定理不要求随机变量本身是正态分布的,所以很容易推测,当在一定条件下,我们可以使用对正态分布成立的方法去应对非正态分布。比如,对样本量n足够大的时候,二项分布 Bin(n, p) 可以用正态分布N(np, np(1-p))来近似等等。
小概率事件
小概率事件即是指发生概率极小的事件,也就是说,在假设检验的思想中,小概率事件在某一次试验中基本上是不会发生的,如果发生了,则说明该实验的原假设出了问题,则应该拒绝原假设。
举个例子,就说抛硬币的问题吧。对于一个正常的抛硬币事件,我们知道其出现正反两面的概率各是50%,假设你跟同学玩抛硬币猜正反面的游戏,结果10次下来,你一次都没赢过。这个时候聪明的你一定开始怀疑这枚硬币是不是有问题,并且你用下面这一段证据狠狠打脸了一下这个同学:
假设检验验证该硬币是否是质地均匀的正常硬币
H0:零假设该硬币是质地均匀的正常硬币 (出现正反面的概率均为50%)
H1:该硬币不是质地均匀的正常硬币
假设H0成立,则每次抛出硬币出现正反面的概率均为0.5,那么抛10次硬币,均出现正面的概率为 0.5^10 = 0.00098,该概率非常小,属于小概率事件,基本不可能出现,如果出现了,则说明零假设H0不正确。所以,我们可以据此否定零假设H0,即“硬币是质地均匀的正常硬币”这一假设不能成立,故而H1成立,硬币不是正常硬币。
从上述小例子可以看出小概率事件的数学思想其实就是用反证法进行假设检验。
差异显著性检验
那中心极限定理和小概率事件等又与我们今天要讨论的差异显著性检验有什么关系呢?
因为假设检验(比如t检验、z检验等)是基于正态分布的一类统计方法,其要求样本数据要符合正态分布。而中心极限定理则为我们提供了理论基础,即根据中心极限定理,无论原始数据是否为正态分布,只要样本容量足够大,抽样样本的均值分布就会接近正态分布。
这样我们就可以对不是正态分布的数据进行差异显著性检验(假设检验)了。
并且,中心极限定理还帮助我们理解如何将样本均值进行标准化,成为标准正态分布(z值),从而可以计算p值(p值的计算过程是基于正态分布的假设,这一部分如果需要,将来会另写一文详细说明)。
在假设检验中,我们通常很关心在零假设H0下会是否会出现极端结果,即小概率事件。而前面的p值,则反映了在零假设成立的前提下,观察到当前或者更极端结果的概率,p值越小,说明观察到的结果越不可能在零假设成立的条件下发生,进而就越充分地拒绝零假设。
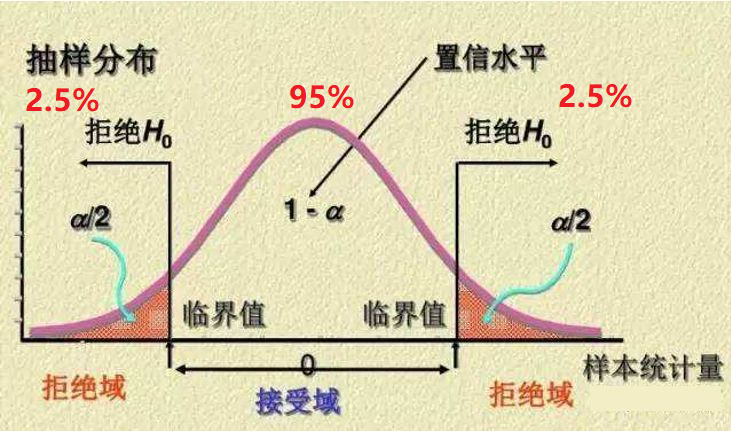
所以,我们可以理解到,当p值足够小的时候,发生的事件就可以认为是小概率事件(如图1所示)。通常,我们可以设定一个显著性水平(比如0.05),如果我们观察到的结果的p值小于设定的显著性水平,那么我们就可以拒绝零假设(例如,在差异显著性检验中,我们的零假设一般是样本之间没有差异)。
在差异显著性检验中,判断差异是否显著的标准,就是看差异是否属于小概率事件,如果差异出现的概率非常低,我们就可以认为这个差异不是偶然的,而是有一定的统计学意义。
到这里,我们基本上清楚了差异显著性检验背后的概率原理了,前面我们已经说过,差异显著性检验包括了好几种检验方法,包括t检验,u检验,卡方检验和方差分析等多种方法,但这次我们只讨论最常用的t检验(t-test)。
t检验
t检验又叫student 检验(学生检验),最早是欧洲一个酒厂的质量检测员,为了观测酿酒品质提出来的统计假说检验,当时酒厂不让随便公开发表文章,这位先生就用了 “student” 这样一个化名发表了,所以后来就又叫student test了,这个故事在《女士品茶》里有详细介绍。
t检验主要用于样本含量较小(比如当样本量n < 30;如果样本量>=30,我们一般更倾向于用z检验)的差异检验。
嗯?前面不是说,当样本量足够大的时候,从任意总体中的抽样样本均值的分布会近似正态分布(中心极限定理),那要是样本量不够大呢?
如果你对概率分布有一些了解的话,你就会知道,对于小样本量的来说,其均值呈现的分布叫t分布,其自由度为df = n - 1。t分布的形状与正态分布相似,其曲线形态随自由度df而改变,df越大,则t分布曲线就越近似正态分布,当自由度df为无穷大时,t分布曲线即为标准正态分布。
好,那接下来我们具体讨论一下最常见的t检验在最常用的excel中的使用。
比如我们现在想要看一下两组数据是不是有差异,如下表所示:
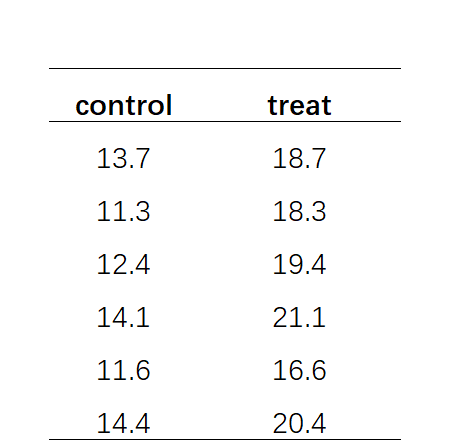
我们使用excel中自带的t检验函数t.test()来检测两组数据是否有差异。Array1输入control这组数据,Array2输入treat这组数据,前面这些数据输入没啥好说的。
需要注意的是,接下来的Tail选项如何选?(如下图所示)
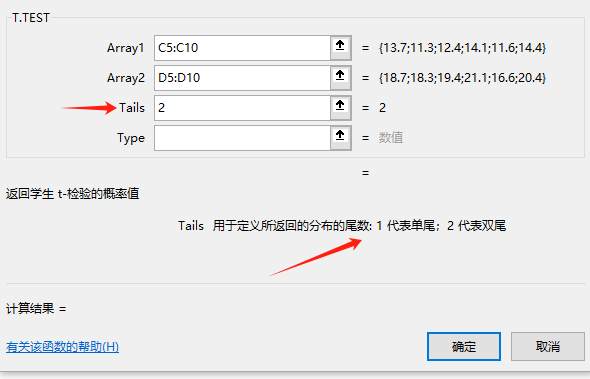
这需要根据你的数据类型和应用场景来设定,在t.test()中,一般分为 ‘单尾’ 和 ‘双尾’ 。
单尾检验和双尾检验都是检验统计显著性的方法,区别在于,单尾检验只检验一个方向的显著性,而双尾检验则检验两个方向的显著性。
举个例子,比如,去年你对一个全社区的10岁以下小孩身高进行了测量,一年后的今年,你又对这批小孩的身高做了测量,因为小孩的身高只有两种可能,要么就今年的比去年的显著增高了,要么就是变化不显著,不可能出现比去年的还显著降低的情况,即身高变化只能是单向的。那在这种情况下,我们就使用单位检验了。
但如果你测量的是两个不同社区 (社区A和社区B) 的小孩身高,这时候,你不确定A是不是一定就比B高,还是B比A高,即其显著变化的方向是双方向的,这种情况下,就使用双尾检验。
我这里提供的数据,是存在双向变化可能的,所以选择的是双尾检验。
设定好了Tail之后,下面还有一个type需要选择(如下图所示)
这里的type通常分为3中类型,即成对检验,双样本等方差假设和双样本异方差检验。
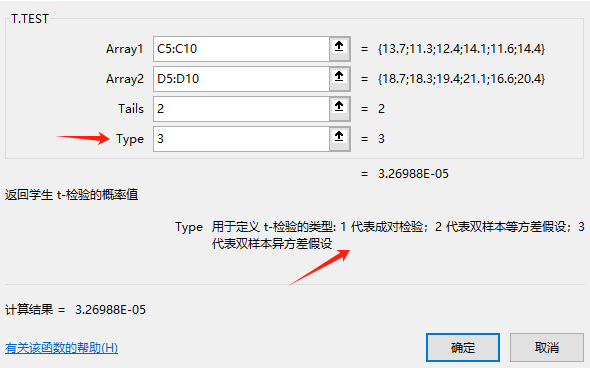
我们先来看成对检验,也就是常说的配对样本t检验。那什么情况下选用配对样本检验呢,
其实这里的配对样本t检验,是与独立样本t检验是相对应的,看名字,我们就大概能知道各自是干嘛的了。还是啰嗦一点,总结一下吧:配对样本检验一般针对的是,观察变量为连续变量,并且两组变量是配对设计的,两组变量是相关的等,而独立样本t检验,则顾名思义就是两组样本是独立的。
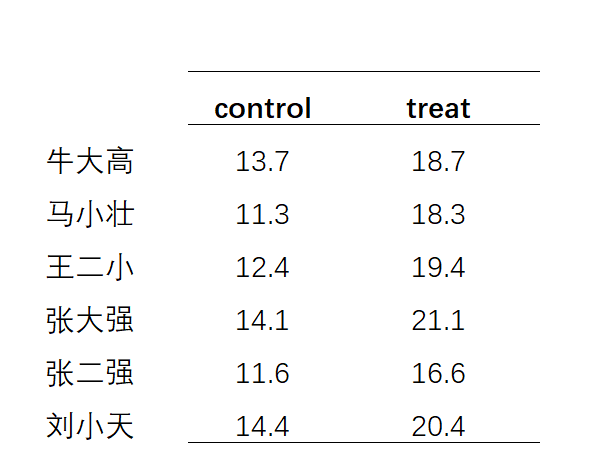
还是前面那组数据,如果我们给每个数据设定为具体的某一个人,就比如这是心脏瓣膜手术后的一组病人,在对其服用华法林之前和连续服用一周后的凝血值进行t检验,这个时候则要用配对样本t检验。
而如果只是随机在医院挑选了两组,服用了华法林的术后病人和没有服用华法林的术后病人,就是这些病人,两批人,这个时候则用独立样本t检验。
接下来我们再来看,什么时候用等方差检验,什么时候用异方差检验?
本质上,其实是在比较两组独立样本均值时,对于这两组样本的方差是否相等的假设。选择哪种假设取决于你对数据的了解,或者你对数据是否满足方差齐性(等方差)假设的检验。
换句话说,当你知道或认为两个样本的方差差异不大时,就使用等方差检验;而当你通过等方差检验(比如 Levene 检验)发现两个样本的方差显著不同,或者你本来就知道样本来源可能具有不同的方差时,这个时候就得使用异方差检验。
但为了减低麻烦,我在处理这类数据前,一般不做方差齐性检验,用眼睛看一下,大概给个估计,就判断二者的方差是不是相近,从而选择做等方差检验还是异方差检验。
上面的这些内容,看起来其实很简单,但在日常工作中,用到的实在太频繁了,因而还是不避其繁地记录了下来。