LASSO回归模型

LASSO 回归模型

.

一. LASSO 回归模型的原理

LASSO 回归（least absolute shrinkage and seletion operator），即最小绝对值收敛和选择算子算法，与最小二乘法在曲线拟合中对参数估计的作用类似，LASSO算法也常被用于广义线性模型中的变量筛选。具体地讲，就是LASSO通过生成一个惩罚函数，对回归模型中的变量系数进行压缩（把不重要的系数压缩到零），从而防止过度拟合，同时保留关键变量，这样可以更好地提高模型的泛化能力。

不管目标因变量是连续的，还是多远离散的，或者是二元的，都可以用LASSO回归进行建模预测。

简单来说，它就是将一个含有很多变量的、复杂线性回归模型进行一定得简化，如下面的方程所示， X¹ 到 Xⁿ 是变量（可以是不同的基因，也可以是不同的剪接事件，可以任何你需要的因素）， β⁰ 是常数项， β¹ 到 βⁿ 是系数（也就是每个变量的权重，不同变量对结局影响的大小）：

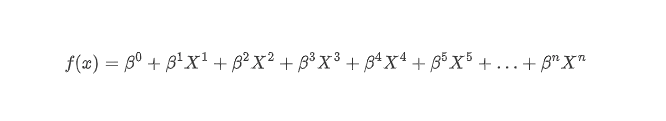
LASSO最大的特点就是引入了惩罚函数λ，对系数β¹ 、β² 、…、以及最后的βⁿ 进行压缩：即当 β¹ = 0 时，X¹ 这个变量对结局的影响就为 0 了，则X¹ 就可以被被剔除出方程：

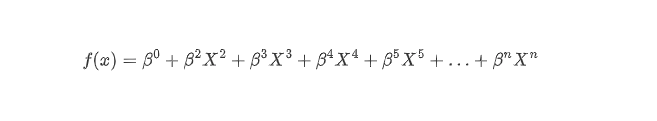
当 β² = 0 时，X²则被剔除方程，……，以此类推，权重越低的变量，越早被压缩到0，逐步压缩之后，最后就会只剩下几个最重要的变量，这里假设是X⁴ 、X⁵ 和 Xⁿ，这时候最后的方程变换为：

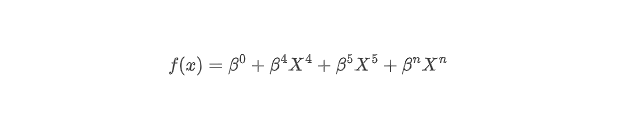
此处所剩下的三个变量X⁴ 、X⁵ 和 Xⁿ 就是我们筛选出来的变量（比如对血管新生影响最大的三个剪接事件），用于下一步分析。

.

.

---

.

二. LASSO = 线性回归 + L1正则化

前面讲了，LASSO回归通过引入了惩罚函数λ，对回归模型中的变量系数进行压缩，从而提高模型的泛化能力。

那具体是如何进行压缩的呢？ 加一个L1正则化项目！

.

在机器学习中，当模型在训练数据上表现良好，却在未见过的其他数据上表现不佳的时，我们称这种情况为过拟合，也就是训练过度了，得到的模型尽可能地满足了训练集数据中的每一个特征，使得模型不仅学习到了数据中真实的潜在规律，同时也记忆了训练数据中的随机波动和噪声，即模型过度适应训练数据中的细节和噪声，这样则会导致模型在新数据上表现（拟合能力）显著下降。

而当模型在未见过的数据中表现良好的时候，我们就说改模型具有较好的概化能力，其反映了模型从训练数据中学习普遍规律而非记忆特定样本的能力，这是评估模型实用价值的核心指标。

.

.

---

.

三. L1正则化

所以，在LASSO回归模型训练中，采用一个L1正则化来将冗余预测变量的系数压缩为0，在压缩系数的同时起到变量筛选的作用，可以避免由于过拟合导致的模型概化能力不足的问题。总结地说，正如前文中所说，LASSO回归其实就是在线性回归的基础上加一个L1正则化项。

这里的L1正则化就是以回归系数的绝对值之和作为惩罚系数，来压缩回归系数。

.

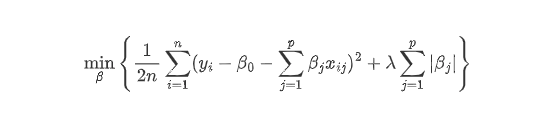
光看上面这个公式好像不太直观，我们举一个贴近一点的例子：比如整理行李箱

假设你要去旅行，但航空公司规定：
行李箱总重量 ≤ 10kg（硬性限制）
必须带最重要的东西（比如证件、手机），可舍弃不重要的（比如多余的鞋子）

L1正则化就像这个行李规则：

1. “总重量” = 所有回归系数绝对值之和（|β₁| + |β₂| + ... + |βₙ|）

2. “10kg限制” = 惩罚强度λ（λ越大，限制越严格）*

3. “扔东西” = 把不重要的变量系数压缩到0（自动筛选关键特征）*

是不是理解更多一些了。

L1正则化就是给模型一个“断舍离”的规则

你可以用很多特征做预测，但所有特征的影响力总和不能超标——必须把不重要的特征影响力降到零！

.

这个LASSO回归公式可以形象地理解为机器学习模型的”双目标优化”，用通俗的语言来拆解它的每个部分：

​

.

左边部分：预测误差

假如你是一位医生，要根据100项体检指标预测糖尿病风险：

• **yᵢ**：第i位患者实际是否患病（是=1，否=0）
• **xᵢⱼ**：第j项检查结果（如血糖=6.5，BMI=28…）
• **βⱼ**：这项检查的”重要性分数”

模型在做的事：

1. 用所有检查结果加权求和（∑βⱼxᵢⱼ）
2. 计算预测值与真实值的差距（误差）
3. 目标：让所有患者的预测误差最小（诊断准确性）

这就是常规机器学习的目标——完美拟合已知数据

.

右边部分：正则化惩罚系数

但100项检查全做不仅太医疗资源，也折腾病人，这里L1正则化就像国家卫健委给医院立规矩：

• **|βⱼ|**：每项检查的”重要性绝对值”
• **λ**：规矩的严格程度（λ越大越抠门）
• 规则：所有检查的”重要性总和”不能超标

实际效果：

• 规矩逐步提高λ（越来越严格）
• 模型被迫放弃不重要的检查（βⱼ=0）
• 最终可能只剩：血糖、胰岛素、BMI等核心指标

.

中间部分：平衡项（加号+）

这个**+**号本质是调节天平：

λ取值	诊断策略	风险
λ=0	用全部100项检查	容易过度诊断（把肥胖纹当糖尿病征兆）
λ适中	精选20项关键检查	既准确又高效
λ过大	只用1-2项检查	可能漏诊重要指标

.

总结就是：

左边：模型的准确性（拟合数据的能力）

右边：模型的简洁性，即惩罚模型复杂度（防止过拟合）

**加号 +*：平衡两者的权重，λ* 决定偏向哪一边。

.

.

---

.

四. LASSO回归系数图和参数图

.

.

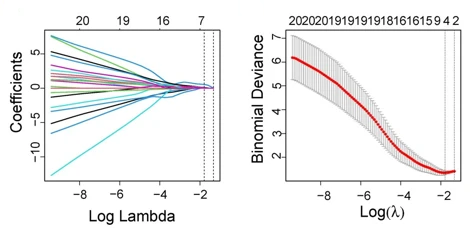
上面这两张图，是LASSO回归中的系数轨迹图（左图）和交叉验证误差图（右图）。

.

在Lasso回归过程中，随着λ的变化，模型中的变量系数、变量个数和模型方差都是在不断变化的。交叉验证误差图展示的是模型均方差是如何随着Log（λ）的变化而变化，用于帮助选择最佳模型。

上方的横坐标，表示对应模型所需变量数目，从左到右逐渐减少；下方的横坐标，是惩罚系数λ的对数；纵坐标表示均方误差（ mean squared error，MSE），其代表计算模型的预测值与真实值的差异程度，每个MSE都有对应的误差棒error bar表示MSE的95%置信区间。

图中有两条虚线，左边的是lambda.min虚线指示最小MSE对应的横坐标，靠右的lambda.1se虚线指距离lambda.min一个标准误的位置，因其包含的变量更少，所以模型更简洁。

在实际应用中若lambda.min与lambda.1se的MSE差别不大，可考虑更简洁模型；

而若差别较大，则根据研究目的选择更准确的lambda.min或更简洁的lambda.1se。从左图可以看出，lambda.min处的候选变量减少到4个。

.

系数轨迹图（左边）展示的是LASSO回归模型减少变量数目和调整系数的过程。

横坐标含义与交叉验证误差图一致，纵轴表示标准化后的回归系数值，其正/负值分别代表正/负相关性。

该图反映了各个变量的重要程度，不同颜色的线代表不同的变量（基因），随着惩罚项λ的增加，一些不重要的变量系数很快就变为0，而越重要的变量，惩罚项对变量系数的影响越小，就越能够留到最后。

如其中的：从右侧持续延伸到左侧（如红线），则代表重要特征；在中间λ时归零（如蓝线）代表的是次要特征；而全程紧贴0轴（未显示）则代表的是噪声特征。

例如此图中lambda.min处有1个变量系数为0，那么剩余7个非零系数的特征变量就是Lasso回归筛选出的变量。

.

结合上述两幅图，假设研究基因与疾病关系：

在左图lambda.1se处画垂直线，与该线相交的基因（假如是Sxl，Rala）即为关键特征。

检查右图对应位置，确认误差接近最小值且模型足够简单。

.

在生物学研究中的常用思路即为：

关键基因列表：在选定λ处非零系数的基因。

效应方向：系数正负号表示促进/抑制疾病。

稳定性验证：通过重采样检查基因是否持续被选中。